RC Phase Shift Oscillator

Analysis of RC Circuit

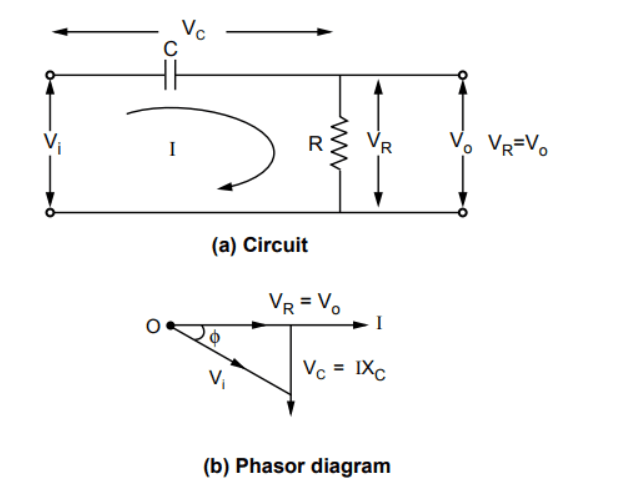
The basic RC network is shown in Fig. (a), with the output taken across the resistor $R$.

• The capacitive reactance $X_C$ is given by: $X_C = \frac{1}{2\pi f C} \text{ Ω}$ where $f$ is the frequency of the input.

• The total impedance of the circuit is: $Z = R - jX_C = R - j\left(\frac{1}{2\pi f C}\right) \text{ Ω}$

  $= |Z|\angle -\phi^\circ \text{ Ω} \quad \text{(i)}$

• The current $I$ flowing in the circuit is: $I = \frac{V_i \angle 0^\circ}{Z} = \frac{V_i \angle 0^\circ}{|Z|\angle -\phi^\circ}$

  $= \frac{V_i}{|Z|}\angle +\phi^\circ \text{ A} \quad \text{(ii)}$

  Therefore: $|Z| = \sqrt{R^2 + X_C^2} \quad \text{and} \quad \phi = \tan^{-1}\left(\frac{X_C}{R}\right)$

  $|Z| = \sqrt{R^2 + X_C^2} \quad \text{and} \quad \phi = \tan^{-1}\left(\frac{X_C}{R}\right)$

The equation (ii) shows that the current $I$ leads the input voltage by angle $\phi$.

• The output voltage $V_o$ is the drop across $R$: $V_o = V_R = I \times R \quad \text{(iii)}$

• The output voltage is in phase with the current, hence it leads the input voltage by angle $\phi$.

• Thus, the RC circuit introduces a phase shift $\phi$ between the input and output, which depends on $R$, $C$, and frequency $f$.

RC Feedback Network for Phase Shift

• In an RC phase shift oscillator, the amplifier introduces a phase shift of $180^\circ$.

• Thus, the feedback network must introduce a phase shift of $180^\circ$ to satisfy the Barkhausen criterion.

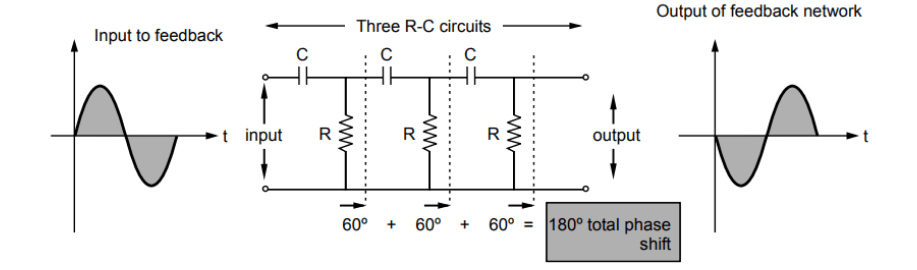
• The RC feedback network consists of three RC sections, each contributing $60^\circ$ phase shift.

• Hence, the feedback network consists of three RC sections, as shown in the figure.

  

• In all three sections, resistance and capacitance values are the same, ensuring each section produces precisely $60^\circ$ phase shift at a particular frequency. This frequency is the operating frequency of the oscillator.

Transistorized RC Phase Shift Oscillator

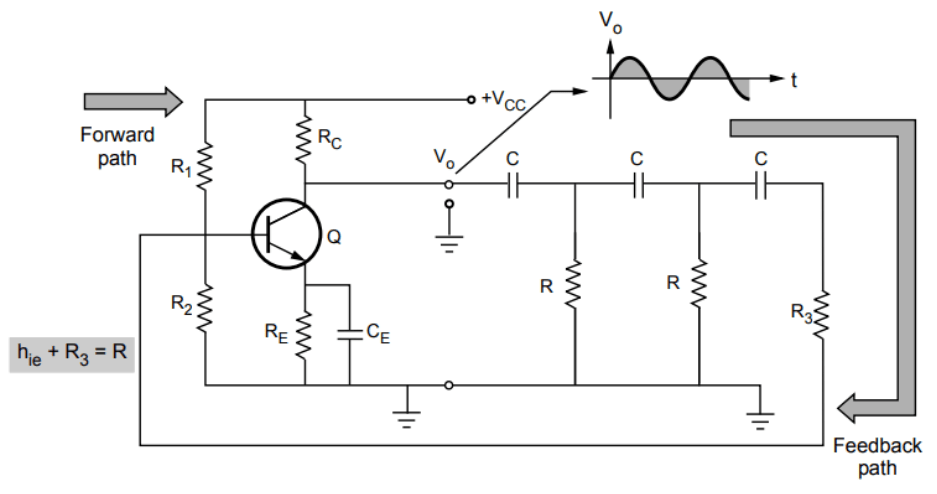
The figure shows an RC phase shift oscillator using a BJT amplifier stage in a common emitter configuration.

• The output of the common emitter amplifier is connected as input to the RC phase-shifting network.

• The output of the RC phase-shifting network is connected as input to the amplifier.

• The common emitter amplifier introduces a phase shift of $180^\circ$ between its input and output.

• The RC phase-shifting network contributes another $180^\circ$ phase shift, making the total phase shift around the loop $360^\circ$.

Neglecting $R_1$ and $R_2$, the input impedance of the amplifier stage is $h_{ie}$:

• To have all three resistance values in the RC sections equal, the resistance in the last section is selected as $R_3$ such that: $R_3 + h_{ie} = R$

  $R_3 = R - h_{ie} \quad \text{(iv)}$

• If $R_1$ and $R_2$ are not neglected: $R_3 = R - [R_1 \parallel R_2 \parallel h_{ie}] \quad \text{(v)}$

• When the gain $A$ of the amplifier stage and feedback factor $\beta$ are adjusted to give $|A \beta | = 1$, the circuit will work as an oscillator, satisfying both the Barkhausen conditions.

Sure, let's go through the derivation of the frequency of oscillations for the RC phase shift oscillator in detail:

Derivation of Frequency of Oscillations

1. Equivalent Circuit:

   Replace the transistor with its approximate $h$-parameter model as shown in the figure.

   

   • The total resistance $R$ in the circuit is given by: $R = h_{ie} + R_3$ where $h_{ie}$ is the input resistance of the transistor, and $R_3$ is the resistance in the RC network.

   • The resistance $R_C$ in the RC network is related to $R$ by a factor $k$: $\frac{R_C}{R} = k$ Thus: $R_C = kR$

   • The modified equivalent circuit is shown below.

     

2. Applying KVL:

   Apply Kirchhoff's Voltage Law (KVL) to the three loops in the circuit:

   • Loop 1 (across $R_C$, $\frac{1}{j\omega C}$, and $R$): $-I_1 R_C - \frac{1}{j\omega C} I_1 - R(I_1 - I_2) - h_{fe} I_b R_C = 0$

     Substituting $R_C = kR$: $-I_1 \left[kR + R + \frac{1}{j\omega C}\right] + I_2 R = h_{fe} I_b kR$

     $-I_1 \left[kR + R + \frac{1}{j\omega C}\right] + I_2 R = h_{fe} I_b kR \quad \text{(vi)}$

   • Loop 2 (across $\frac{1}{j\omega C}$, $R$, and $R$): $-\frac{1}{j\omega C} I_2 - R(I_2 - I_1) - R(I_2 - I_3) = 0$

     $I_1 R - I_2 \left(2R + \frac{1}{j\omega C}\right) + I_3 R = 0$

     $I_1 R - I_2 \left(2R + \frac{1}{j\omega C}\right) + I_3 R = 0 \quad \text{(vii)}$

   • Loop 3 (across $\frac{1}{j\omega C}$, $R$, and $R$): $-\frac{1}{j\omega C} I_3 - I_3 R - R(I_3 - I_2) = 0$

     $I_2 R - I_3 \left(2R + \frac{1}{j\omega C}\right) = 0$

     $I_2 R - I_3 \left(2R + \frac{1}{j\omega C}\right) = 0 \quad \text{(viii)}$

3. Solving Using Cramer's Rule:

   Construct the determinant $D$ from the above equations:

   $D = \begin{vmatrix} -(k+1)R - \frac{1}{sC} & +R & 0 \\ R & -2R - \frac{1}{sC} & R \\ 0 & R & -2R - \frac{1}{sC} \end{vmatrix}$

   Solving this determinant:

   $D = -\frac{s^3 C^3 R^3 (3k+1) + s^2 C^2 R^2 (4k+6) + sRC(5+k) + 1}{s^3 C^3}$ $\quad \text{(ix)}$

   Find $D_3$ to solve for $I_3$:

   $D_3 = \begin{vmatrix} -(k+1)R - \frac{1}{sC} & R & h_{fe} I_b kR \\ R & -2R - \frac{1}{sC} & 0 \\ 0 & R & 0 \end{vmatrix} =$

   $kR^3 h_{fe} I_b$

   $D_3 = kR^3 h_{fe} I_b \quad \text{(x)}$

   Therefore:

   $I_3 = \frac{D_3}{D} = \frac{-kR^3 h_{fe} I_b s^3 C^3}{s^3 C^3 R^3 (3k+1) + s^2 C^2 R^2 (4k+6) + sRC(5+k) + 1}$

   $\quad \text{(xi)}$

   The transistor current gain $h_{fe}$ and $\beta$ are related by:

   $\beta = \frac{I_3}{h_{fe} I_b}$

   $A = \frac{I_3}{I_b} = h_{fe}$

   Therefore:

   $A \beta = h_{fe} \times \frac{I_3}{h_{fe} I_b} = \frac{I_3}{I_b}$

   $A \beta = \frac{I_3}{I_b} \text{ (xii)}$

4. Frequency Calculation:

   From equations (xii) and (xi),

   $A \beta \quad = \quad \frac{-k \ R^3 \ h_{fe} \ s^3 C^3}{s^3 C^3 R^3 (3k+1) + s^2 C^2 R^2 (4k+6) + sRC(5+k) + 1}$

   $\quad \text{(xiii)}$

   Using $s = j\omega, \; \; \; \; \; \; s^2 = +j^2 \omega^2 = -\omega^2, \; \; \; \; \; \; s^3 = j^3 \omega^3 = -j\omega^3$ and

   Separating the real and imaginary parts we get,

   $A \beta = \frac{+ j\omega^3 \ k \ R^3 \ C^3 \ h_{fe}}{[1 - 4 \ k \ \omega^2 C^2 R^2 - 6 \ \omega^2 C^2 R^2] - j \ \omega [3 \ k \omega^2 R^3 C^3 + \omega^2 R^3 C^3 - 5 RC - kRC]}$

   Dividing numerator and denominator by $\ j\omega^3 R^3 C^3$ and replacing $\ -\frac{1}{j}= +j$

   $A\beta = \frac{k h_{fe}}{-j \left\{ \frac{1}{\omega^3 R^3 C^3} - \frac{4k}{\omega RC} - \frac{6}{\omega RC} \right\} - \left\{ 3k + 1 - \frac{5}{\omega^2 R^2 C^2} - \frac{k}{\omega^2 R^2 C^2} \right\}}$

   $\therefore \; \; A \beta = \frac{k h_{fe}}{-\left[3 - 3k - 1 + 5 \alpha^2 + k \alpha^2\right] - j \left[\alpha^3 - 4k \alpha - 6 \alpha\right]} \quad \text{(xiv)}$

   where $\alpha = \frac{1}{\omega RC}$.

   To satisfy the Barkhausen criterion ($\angle A\beta = 0^\circ$), the imaginary part must be zero:

   $\alpha^3 - 4k \alpha - 6 \alpha = 0$

   $\alpha(\alpha^2 - 4k - 6) = 0$

   $\alpha^2 = 4k + 6$

   $\frac{1}{\omega RC} = \sqrt{4k + 6}$

   $\omega = \frac{1}{RC \sqrt{4k + 6}}$

   $f = \frac{1}{2 \pi RC \sqrt{4k + 6}}$

   Thus, the frequency of oscillations is:

   $f = \frac{1}{2 \pi RC \sqrt{4k + 6}} \quad \text{(xv)}$

   Minimum Value of $h_{fe}$:

   Substituting $\alpha = \sqrt{4k + 6}$ in equation (xiv),

   $A\beta = \frac{k h_{fe}}{-3k - 1 + (4k + 6)(5 + k)} = \frac{k h_{fe}}{4k^2 + 23k + 29}$

   For $|A \beta| = 1$:

   $\frac{k h_{fe}}{4k^2 + 23k + 29} = 1$

   $h_{fe} = 4k + 23 + \frac{29}{k}$

   To find the minimum value of $h_{fe}$, differentiate with respect to $k$:

   $\frac{d}{dk} \left[ 4k + 23 + \frac{29}{k} \right] = 0$

   $4 - \frac{29}{k^2} = 0$

   $k^2 = \frac{29}{4}$

   $k = 2.6925 \text{ for minimum } h_{fe}$

   Substituting $k = 2.6925$:

   $h_{fe(min)} = 4 \times 2.6925 + 23 + \frac{29}{2.6925} = 44.54$

   Thus, the transistor must have $h_{fe} \geq 44.54$ for the circuit to oscillate.

Advantages of RC Phase Shift Oscillator

• The circuit is simple to design.
• Can produce output over the audio frequency range.
• Produces a sinusoidal output waveform.
• It is a fixed-frequency oscillator.

Disadvantages of RC Phase Shift Oscillator

• To vary the frequency, the values of the resistors (R) and capacitors (C) in all three sections need to be adjusted simultaneously, which is practically difficult. Hence, the frequency cannot be easily varied.
• Frequency stability is poor due to changes in component values caused by factors such as temperature variations and aging.