Stacks - HPTU Exam Helper

Representation of Stack in Memory

A stack is a linear data structure that follows the LIFO (Last In, First Out) principle, meaning the last element inserted is the first to be removed. Both insertion and deletion operations happen at one end only.

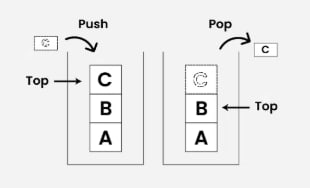
Since the stack follows the LIFO principle, the element that is pushed last is popped first.

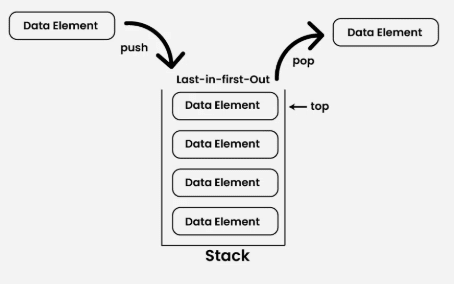
Types of Stack:

Fixed Size Stack: As the name suggests, a fixed size stack has a predefined capacity and cannot grow or shrink dynamically. If the stack is full and an attempt is made to add an element, an overflow error occurs. If the stack is empty and an attempt is made to remove an element, an underflow error occurs.
Dynamic Size Stack: A dynamic size stack can grow or shrink dynamically. When the stack is full, it automatically increases its size to accommodate a new element, and when it's empty, it reduces its size. This type of stack is typically implemented using a linked list, which allows for easy resizing.

Implementation of Stack Using an Array

A stack is a linear data structure that follows the LIFO principle. To implement a stack using an array, initialize an array and treat its end as the stack’s top. Implement push (add to end), pop (remove from end), and peek (check end) operations, handling cases for an empty or full stack.

Step-by-step approach:

Initialize an array to represent the stack.
Use the end of the array to represent the top of the stack.
Implement push (add to end), pop (remove from end), and peek (check end) operations, ensuring to handle empty and full stack conditions.

// C++ program to create a stack with given capacity
#include <bits/stdc++.h>
using namespace std;
 
class Stack {
    int top, cap;
    int* a;
 
public:
    Stack(int cap) {
        this->cap = cap;
        top = -1;
        a = new int[cap];
    }
 
    ~Stack() {
        delete[] a;
    }
 
    bool push(int x) {
        if (top >= cap - 1) {
            cout << "Stack Overflow\n";
            return false;
        }
        a[++top] = x;
        return true;
    }
 
    int pop() {
        if (top < 0) {
            cout << "Stack Underflow\n";
            return 0;
        }
        return a[top--];
    }
 
    int peek() {
        if (top < 0) {
            cout << "Stack is Empty\n";
            return 0;
        }
        return a[top];
    }
 
    bool isEmpty() {
        return top < 0;
    }
};
 
int main() {
    Stack s(5);
    s.push(10);
    s.push(20);
    s.push(30);
    cout << s.pop() << " popped from stack\n";
 
    cout << "Top element is: " << s.peek() << endl;
 
    cout << "Elements present in stack: ";
    while (!s.isEmpty()) {
        cout << s.peek() << " ";
        s.pop();
    }
 
    return 0;
}

Output

30 popped from stack
Top element is: 20
Elements present in stack: 20 10

Implementation of Stack Using a Linked List

To implement a stack using a singly linked list, all operations must follow the LIFO (Last In, First Out) principle, where the most recently added element is the first to be removed. In this approach, each node contains data and a reference to the next node.

We maintain a top pointer that always points to the most recent (topmost) node in the stack. The key stack operations—push, pop, and peek—are performed using this pointer.

Stack Operations

push(): Insert a new element at the beginning of the linked list.
pop(): Remove the first element from the linked list.
peek(): Return the top element.
display(): Print all elements in the stack.

#include <bits/stdc++.h>
using namespace std;
 
class Node {
public:
    int data;
    Node* next;
    Node(int new_data) {
        this->data = new_data;
        this->next = nullptr;
    }
};
 
class Stack {
    Node* head;
 
public:
    Stack() { this->head = nullptr; }
 
    bool isEmpty() {
        return head == nullptr;
    }
 
    void push(int new_data) {
        Node* new_node = new Node(new_data);
        if (!new_node) {
            cout << "\nStack Overflow";
        }
        new_node->next = head;
        head = new_node;
    }
 
    void pop() {
        if (this->isEmpty()) {
            cout << "\nStack Underflow" << endl;
        } else {
            Node* temp = head;
            head = head->next;
            delete temp;
        }
    }
 
    int peek() {
        if (!isEmpty())
            return head->data;
        else {
            cout << "\nStack is empty";
            return INT_MIN;
        }
    }
};
 
int main() {
    Stack st;
 
    st.push(11);
    st.push(22);
    st.push(33);
    st.push(44);
 
    cout << "Top element is " << st.peek() << endl;
 
    cout << "Removing two elements..." << endl;
    st.pop();
    st.pop();
 
    cout << "Top element is " << st.peek() << endl;
 
    return 0;
}

Output

Top element is 44
Removing two elements...
Top element is 22

Time Complexity: O(1) for all push(), pop(), and peek() operations, as no traversal is needed.

Auxiliary Space: O(n), where n is the size of the stack.

Implementation of Stack Using Deque

A double-ended queue or deque allows insertion and deletion at both ends. In a stack, we perform insertions and deletions at only one end. We can use either end of the deque (front or back) to implement a stack.

In the implementation below, we use the back (or rear) of the deque for both insertions and deletions. Note that the time complexities of all operations (insertions and deletions at both ends) in a deque are O(1). Hence, the time complexity of the implementation below is O(1).

In Java, the deque implementation of a stack is preferred over the standard Stack class because the Stack class is a legacy class mainly designed for multithreaded environments.
In Python, there is no standard stack class, so we can use either a list or deque. The deque implementation is preferred because it is optimized for insertions and deletions at both ends.

#include <iostream>
#include <deque>
 
using namespace std;
 
int main() {
    deque<int> stack;
 
    stack.push_back(10);
    stack.push_back(20);
    stack.push_back(30);
 
    cout << stack.back() << " popped from deque" << endl;
    stack.pop_back();
    cout << "Top element is: " << stack.back() << endl;
    return 0;
}

Output

30 popped from deque
Top element is: 20

Operations on Stack and Applications

To manipulate a stack, certain standard operations are available:

push() to insert an element into the stack
pop() to remove an element from the stack
top() or peek() to return the top element of the stack
isEmpty() returns true if the stack is empty, otherwise false
isFull() returns true if the stack is full, otherwise false

To implement a stack, we need to maintain a reference to the top element.

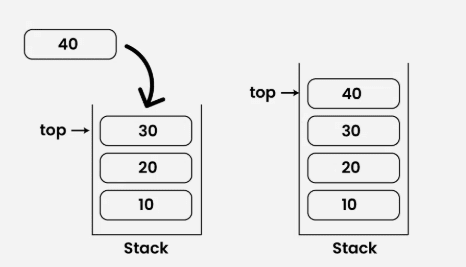
Push Operation on Stack

Adds an item to the stack. If the stack is full, it results in an overflow condition.

Algorithm for Push Operation:

Check if the stack is full.
If the stack is full (top == capacity - 1), a Stack Overflow occurs and the element cannot be inserted.
Otherwise, increment top by 1 (top = top + 1) and insert the new element at the top position.
Elements can be pushed until the stack reaches its capacity.

Pop Operation on Stack

Removes an item from the stack. Elements are popped in the reverse order of their insertion. If the stack is empty, it results in an underflow condition.

Algorithm for Pop Operation:

Check if the stack is empty.
If the stack is empty (top == -1), a Stack Underflow occurs and no element can be removed.
Otherwise, store the value at top, decrement top by 1 (top = top - 1), and return the stored value.

Top or Peek Operation on Stack

Returns the top element of the stack.

Algorithm for Top Operation:

Check if the stack is empty.
If the stack is empty (top == -1), print “Stack is empty”.
Otherwise, return the element at index top.

isEmpty Operation in Stack Data Structure

Returns true if the stack is empty, otherwise false.

Algorithm for isEmpty Operation:

Check the value of top.
If top == -1, the stack is empty; return true.
Otherwise, return false.

isFull Operation in Stack Data Structure

Returns true if the stack is full, otherwise false.

Algorithm for isFull Operation:

Check the value of top.
If top == capacity - 1, the stack is full; return true.
Otherwise, return false.

Applications of Stacks

Function calls: Stacks store return addresses during function calls to ensure the program returns to the correct location after execution.
Recursion: Used to manage local variables and return addresses in recursive calls.
Expression evaluation: Useful for evaluating expressions in postfix (Reverse Polish) notation.
Syntax parsing: Helps validate the syntax in programming and formal languages.
Memory management: Assists in memory allocation and management in operating systems and some languages.
Problem-solving: Used in solving problems like Next Greater Element, Previous Greater Element, Next Smaller Element, Previous Smaller Element, Largest Rectangle in Histogram, and Stock Span Problem.

Advantages of Stacks:

Simplicity: Easy to understand and use.
Efficiency: Push and pop operations take constant time, O(1).
LIFO behavior: Ensures the most recently added item is removed first, ideal for function calls and expression evaluation.
Memory efficiency: Uses only as much memory as needed to store current elements.

Disadvantages of Stacks:

Limited access: Only the top element can be accessed or modified.
Overflow potential: In fixed-size stacks, inserting too many elements causes overflow and data loss.
No random access: Elements cannot be accessed in arbitrary order.
Fixed capacity: Not suitable for scenarios where the required size is highly variable unless implemented dynamically.

How's article quality?

Page Contents