Queues - HPTU Exam Helper

Representation of Queue in Memory

A queue is a linear data structure that follows the FIFO (First In First Out) principle, meaning the first element inserted is the first to be removed.

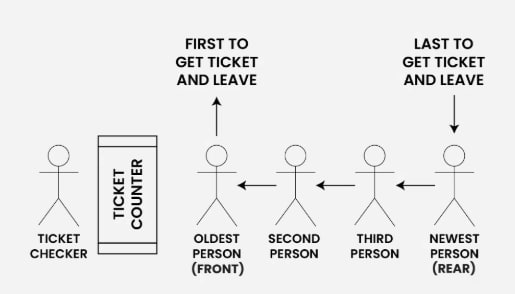
The FIFO principle states that the first element added to the queue will be the first one to be removed or processed. A queue is similar to a line of people waiting to purchase tickets, where the first person in line is the first one served (i.e., First Come First Serve).

Front: The position of the element ready to be served (i.e., the first element to be removed from the queue) is called the front of the queue. It is also referred to as the head of the queue.
Rear: The position of the last element in the queue (i.e., the most recently added element) is called the rear of the queue. It is also referred to as the tail of the queue.
Size: Refers to the current number of elements in the queue.
Capacity: Refers to the maximum number of elements the queue can hold.

Types of Queues

The queue data structure can be classified into four types:

Simple Queue: Follows the FIFO principle. Elements can be inserted only at the rear and removed only from the front. It can be efficiently implemented using a linked list or a circular array.
Double-Ended Queue (Deque): In a deque, insertion and deletion operations can be performed from both ends. There are two subtypes:
- Input-Restricted Queue: In this type, input is allowed only at one end, but deletion can be done from both ends.
- Output-Restricted Queue: In this type, input is allowed at both ends, but deletion can be done only from one end.
Priority Queue: A special type of queue where elements are accessed based on assigned priorities.
- Ascending Priority Queue: Elements are arranged in increasing order of priority. The element with the smallest priority value is removed first.
- Descending Priority Queue: Elements are arranged in decreasing order of priority. The element with the highest priority is removed first.

Operations on Queues

A queue is a linear data structure that follows the FIFO (First In First Out) principle, meaning the first element inserted is the first to be removed.

Some of the basic operations in a queue data structure are:

enqueue() – Insertion of elements into the queue.
dequeue() – Removal of elements from the queue.
getFront() – Returns the element at the front of the queue without removing it.
getRear() – Returns the element at the rear of the queue without removing it.
isFull() – Checks whether the queue is full.
isEmpty() – Checks whether the queue is empty.
size() – Returns the number of elements currently in the queue.

Operation 1: enqueue()

Inserts an element at the rear end of the queue.

Steps to perform enqueue:

Check if the queue is full.
If full, return an overflow error and exit.
If not full, increment the rear pointer to point to the next empty space.
Add the element to the position indicated by the rear.
Return success.

Operation 2: dequeue()

Removes and returns the element at the front of the queue.

Steps to perform dequeue:

Check if the queue is empty.
If empty, return an underflow error and exit.
If not empty, access the element at the front.
Increment the front pointer to the next element.
Return success.

Operation 3: getFront()

Returns the element at the front of the queue without removing it.

Steps to perform getFront():

If the queue is empty, return a default minimum value (e.g., -1).
Otherwise, return the front element.

Operation 4: getRear()

Returns the element at the rear of the queue without removing it.

Steps to perform getRear():

If the queue is empty, return a default minimum value.
Otherwise, return the rear element.

Operation 5: isEmpty()

Returns a boolean indicating whether the queue is empty.

Steps to perform isEmpty():

If the front is equal to -1, return true (queue is empty).
Otherwise, return false.

Operation 6: size()

Returns the number of elements currently in the queue.

Code Implementation of All Operations:

#include <iostream>
#include <queue>
using namespace std;
 
queue<int> q;
 
bool isEmpty()
{
    return q.empty();
}
 
void qEnqueue(int data)
{
    q.push(data);
}
 
void qDequeue()
{
    if (isEmpty()) {
        return;
    }
    q.pop();
}
 
int getFront()
{
    if (isEmpty()) return -1;
    return q.front();
}
 
int getRear()
{
    if (isEmpty()) return -1;
    return q.back();
}
 
int main()
{
    qEnqueue(1);
    qEnqueue(8);
    qEnqueue(3);
    qEnqueue(6);
    qEnqueue(2);
 
    if (!isEmpty()) {
        cout << "Queue after enqueue operation: ";
        queue<int> tempQueue = q; 
        while (!tempQueue.empty()) {
            cout << tempQueue.front() << " ";
            tempQueue.pop();
        }
        cout << endl;
    }
 
    cout << "Front: " << getFront() << endl;
    cout << "Rear: " << getRear() << endl;
 
    cout << "Queue size: " << q.size() << endl;
 
    qDequeue();
 
    cout << "Is queue empty? " << (isEmpty() ? "Yes" : "No") << endl;
 
    return 0;
}

Output

Queue after enqueue operation: 1 8 3 6 2 
Front: 1
Rear: 2
Queue size: 5
Is queue empty? No

Circular Queues

A circular queue is a special type of queue in data structures where the last position is connected back to the first position, forming a circle.

This means that when the queue reaches the end, it wraps around to the beginning. This helps utilize all available space efficiently without leaving any gaps.

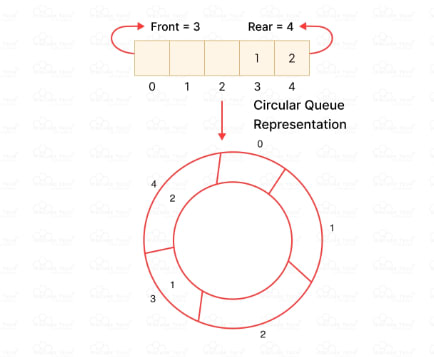
For example, if you keep adding items to a circular queue, it will fill up from the start again after reaching the end. This is useful for tasks like managing waiting lists or buffering data in a computer system, ensuring no space is wasted.

Circular Queue Operations

Circular queues have several key operations that allow for the efficient management of elements:

1. Enqueue (Adding an element)

Add an element to the rear of the circular queue.

Steps:

Check if the queue is full. If (rear + 1) % capacity == front, the queue is full.
If the queue is not full, update the rear pointer to (rear + 1) % capacity.
Insert the new element at the rear position.
If the queue was initially empty (i.e., front was -1), set front to 0.

void enqueue(int item) {
    if (isFull()) {
        cout << "Queue is full!" << endl;
        return;
    }
    if (front == -1) {
        front = 0;
    }
    rear = (rear + 1) % capacity;
    arr[rear] = item;
}

2. Dequeue (Removing an element)

Remove an element from the front of the circular queue.

Steps:

Check if the queue is empty. If front == -1, the queue is empty.
If the queue is not empty, remove the element at the front position.
Update the front pointer to (front + 1) % capacity.
If the queue becomes empty after the dequeue operation (i.e., front equals rear), reset both front and rear to -1.

int dequeue() {
       if (isEmpty()) {
           cout << "Queue is empty!" << endl;
           return -1;
       }
       int item = arr[front];
       if (front == rear) {
           front = -1;
           rear = -1;
       } else {
           front = (front + 1) % capacity;
       }
       return item;
}

3. Peek/Front (Viewing the front element)

View the front element without removing it from the circular queue.

Steps:

Check if the queue is empty. If front == -1, the queue is empty.
If the queue is not empty, return the element at the front position.

int peek() {
    if (isEmpty()) {
        cout << "Queue is empty!" << endl;
        return -1;
    }
    return arr[front];
}

4. isEmpty (Checking if the queue is empty)

Check if the circular queue is empty.

Steps:

The queue is empty if front == -1.

bool isEmpty() {
    return front == -1;
}

5. isFull (Checking if the queue is full)

Check if the circular queue is full.

Steps:

The queue is full if (rear + 1) % size == front.

bool isFull() {
    return (rear + 1) % capacity == front;
}

Implementation:

#include <iostream>
using namespace std;
 
#define MAX 100
 
class CircularQueue {
    int arr[MAX];
    int front;
    int rear;
    int capacity;
 
public:
    CircularQueue(int size) {
        capacity = size;
        front = -1;
        rear = -1;
    }
 
    void enqueue(int item) {
        if (isFull()) {
            cout << "Queue is full!" << endl;
            return;
        }
        if (front == -1) {
            front = 0;
        }
        rear = (rear + 1) % capacity;
        arr[rear] = item;
    }
 
    int dequeue() {
        if (isEmpty()) {
            cout << "Queue is empty!" << endl;
            return -1;
        }
        int item = arr[front];
        if (front == rear) {
            front = -1;
            rear = -1;
        } else {
            front = (front + 1) % capacity;
        }
        return item;
    }
 
    int peek() {
        if (isEmpty()) {
            cout << "Queue is empty!" << endl;
            return -1;
        }
        return arr[front];
    }
 
    bool isEmpty() {
        return front == -1;
    }
 
    bool isFull() {
        return (rear + 1) % capacity == front;
    }
};
 
int main() {
    CircularQueue cq(5);
    cq.enqueue(1);
    cq.enqueue(2);
    cq.enqueue(3);
    cout << "Dequeued element: " << cq.dequeue() << endl;  // Output: 1
    cout << "Front element: " << cq.peek() << endl;        // Output: 2
    cout << "Is empty: " << cq.isEmpty() << endl;          // Output: 0 (false)
    cout << "Is full: " << cq.isFull() << endl;            // Output: 0 (false)
    return 0;
}

Advantages of Circular Queue

Efficient Use of Space

Circular queues make efficient use of available space by allowing the rear pointer to wrap around to the front when the end of the array is reached. This ensures no space is wasted, unlike in a linear queue where space can be left unused after elements are dequeued.
No Need for Shifting Elements

In a linear queue, when an element is dequeued, all other elements need to be shifted one position forward to maintain the order. This shifting operation is not required in a circular queue, as the circular nature takes care of the order, resulting in faster operations.
Fixed Size

Circular queues are implemented using a fixed-size array, which simplifies memory management. The size of the queue is determined at the time of creation, avoiding the need for dynamic resizing and memory reallocation.
Consistent Time Complexity

Enqueue and dequeue operations in a circular queue both have a consistent time complexity of O(1). This means that the time taken for these operations is constant and does not depend on the number of elements in the queue, leading to predictable performance.
Better Performance in Buffer Management

Circular queues are widely used in buffering scenarios, such as in streaming applications or operating system task scheduling. They provide a smooth and efficient way to manage buffers, avoiding buffer overflows and underflows effectively.
Ideal for Resource Management

Circular queues are useful in scenarios where resources need to be managed in a cyclic manner, such as round-robin scheduling in operating systems. They ensure that each resource is given equal time and processed in a cyclic order.
Simple Implementation

The logic for implementing circular queues is straightforward and easy to understand. Using modulo operations to wrap around indices simplifies the code and reduces the potential for errors.

Double Ended Queues

A deque, or double-ended queue, is a generalized version of the queue data structure that allows insertion and deletion at both ends. Below is an example program of a deque in different languages.

A deque can act as both a stack and a queue.
It is useful in many problems where we need a subset of all operations, such as insert/remove at the front and insert/remove at the rear.
It is typically implemented using either a doubly linked list or a circular array.

A double-ended queue, often called a deque, is a versatile data structure that allows insertion and deletion of elements from both the front and rear ends. Unlike a standard queue, which follows a First-In, First-Out (FIFO) principle, a deque can function in both FIFO and Last-In, First-Out (LIFO) modes. This flexibility makes it suitable for various applications where dynamic size and efficient access to both ends are required.

Key Characteristics of a Deque:

Insertion and Deletion: Elements can be added or removed from either the front (head) or the rear (tail) of the deque.
Hybrid Nature: Deques combine the functionalities of both stacks and queues, offering more flexibility than either one alone.
Implementation: Deques can be implemented using arrays or linked lists, each with its own performance characteristics.
Dynamic Size: Deques can dynamically grow or shrink as needed, making them suitable for situations where the number of elements is not fixed.

Operations on a Deque:

insertFront(): Adds an element at the front of the deque.
insertRear(): Adds an element at the rear of the deque.
deleteFront(): Removes an element from the front of the deque.
deleteRear(): Removes an element from the rear of the deque.

Examples of Deque Usage:

Process Scheduling: In operating systems, deques can be used to manage processes in a way that prioritizes certain tasks or allows processes to steal resources from others.
Palindrome Detection: Deques can efficiently check if a string is a palindrome by allowing insertion and deletion from both ends.
External Sorting: Deques can be used in external sorting algorithms to handle large datasets that cannot fit in memory at once.
Implementing Stacks and Queues: Deques can be used to implement stacks (LIFO) and queues (FIFO) by restricting operations to one end.
Undo/Redo Functionality: In text editors or other applications, deques can be used to store a history of actions, allowing users to undo or redo changes.

Implementation

#include <iostream>
#include <deque>
 
using namespace std;
 
int main() {
    deque<int> dq;
 
    dq.push_back(10);
    dq.push_back(20);
    dq.push_front(30);
 
    // Print deque elements
    for (int x : dq) cout << x << " ";
    cout << endl;
 
    // Pop from front and back
    dq.pop_front();
    dq.pop_back();
 
    // Print deque elements after pop
    for (int x : dq) cout << x << " ";
    
    return 0;
}

30 10 20 
10

Priority Queues

A priority queue is a type of queue that arranges elements based on their priority values.

Each element has an associated priority. When an item is added, it is inserted based on its priority.
Elements with higher priority are typically retrieved or removed before elements with lower priority.
A binary heap is the most common method to implement a priority queue. In binary heaps, we have easy access to the minimum (in a min heap) or maximum (in a max heap), and since a binary heap is a complete binary tree, it can be easily implemented using arrays. Using arrays also provides a cache-friendly advantage.
Priority queues are used in algorithms such as Dijkstra’s algorithm, Prim’s algorithm, and Huffman coding.

For example, in the below priority queue, an element with the highest ASCII value will have the highest priority. Elements with higher priority are served first.

Types of Priority Queues

Ascending Order Priority Queue: In this queue, elements with lower values have higher priority. For example, with elements 4, 6, 8, 9, and 10, 4 will be dequeued first since it has the smallest value.
Descending Order Priority Queue: Elements with higher values have higher priority. The root of the heap is the highest element and is dequeued first. The queue adjusts itself by maintaining the heap property after each insertion or deletion.

Operations on a Priority Queue

A typical priority queue supports the following operations:

Insertion: If the newly inserted item has the highest priority, it is placed at the top. Otherwise, it is inserted in such a way that it becomes accessible only after all higher-priority items are accessed.
Deletion: We typically remove the highest priority item, which is usually at the top. Once we remove this item, we do not need to move the next priority item manually to the top.
Peek: This operation returns the highest priority item (usually at the top) without modifying the priority queue.

#include <iostream>
#include <queue>
using namespace std;
 
int main() {
    
    // Creating a priority queue of integers
    priority_queue<int> pq;
    pq.push(9);
    pq.push(10);
    pq.push(6);
    
    cout << pq.top() << " ";
    return 0;
}

Output

Explanation: In the above program, we created a priority queue of integers containing the elements 9, 10, and 6. The top element, which is the largest value in the queue, is then printed.

Syntax

priority_queue<T, c, comp> pq;

priority_queue is defined as std::priority_queue inside the <queue> header file. Where:

T: Type of elements in the priority queue.
pq: Name assigned to the priority queue.
c: Underlying container (defaults to vector).
comp: A binary predicate function that tells the priority queue how to compare two elements. This is used to set a custom priority rule. It is optional; if not provided, the highest value gets the highest priority.

Applications

Applications of Queues in Operating Systems:

Semaphores
FCFS (First Come First Serve) scheduling, e.g., FIFO queue
Spooling in printers
Buffers for devices like keyboards
CPU scheduling
Memory management

Applications of Queues in Networks:

Queues in routers/switches
Mail queues
Variations such as Deque, Priority Queue, Doubly Ended Priority Queue

Other Applications of Queues:

Waiting lists for a single shared resource like CPU, disk, or printer
Buffers in MP3 players and portable CD players
Handling interrupts in operating systems
Adding a song to the end of a playlist or playing from the front
WhatsApp message queuing when the recipient is offline
Traffic software (each light turns on one by one at set intervals)

Issues in Queue Applications:

Queue Overflow: A fixed-size queue can become full if elements are added faster than removed. Solutions include dynamic resizing or circular buffers.
Queue Underflow: Removing an element from an empty queue leads to underflow. This is prevented using null pointers or sentinel values.
Blocking Queues: A queue may block when full or empty, leading to delays or deadlocks. Bounded or non-blocking queues help address this.
Priority Inversion: A higher-priority element may get stuck behind a lower-priority one, reducing performance. Priority queues or multi-level queues can help prevent this.
Synchronization Issues: Concurrent access by multiple threads can cause race conditions or deadlocks. Use of mutexes or semaphores resolves this.
Memory Management: Frequent memory allocation and deallocation can lead to fragmentation. Memory pools or pre-allocated buffers are used to improve performance.

How's article quality?

Representation of Queue in Memory

Operations on Queues

Circular Queues

Double Ended Queues

Priority Queues

Applications

Page Contents