Trees - HPTU Exam Helper

Introduction

A tree data structure is a hierarchical structure used to represent and organize data in the form of a parent-child relationship. The following are some real-world situations that naturally resemble a tree:

Folder structure in an operating system
Tag structure in an HTML (with the root tag as <html>) or XML document

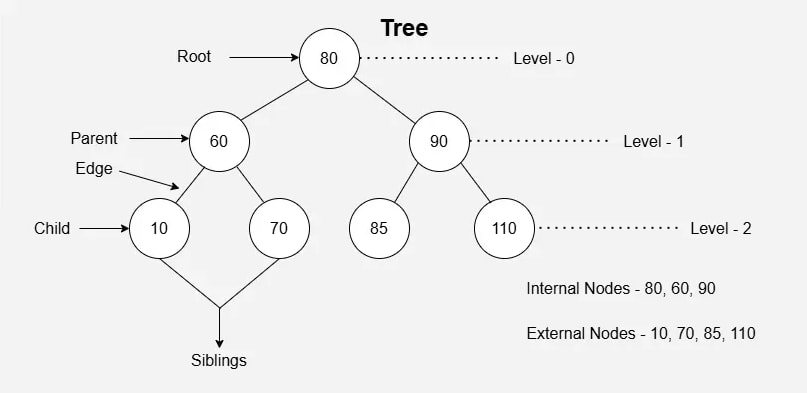
The topmost node of the tree is called the root, and the nodes below it are called child nodes. Each node can have multiple child nodes, and these child nodes can also have their own child nodes, forming a recursive structure.

Parent Node: The node that is the immediate predecessor of a node is called its parent node. {B} is the parent node of {D, E}.
Child Node: The node that is the immediate successor of a node is called its child node. Examples: {D, E} are the child nodes of {B}.
Root Node: The topmost node of a tree, or the node that does not have any parent node, is called the root node. {A} is the root node of the tree. A non-empty tree must contain exactly one root node and exactly one path from the root to all other nodes in the tree.
Leaf Node or External Node: Nodes that do not have any child nodes are called leaf nodes. {I, J, K, F, G, H} are the leaf nodes of the tree.
Ancestor of a Node: Any predecessor node on the path from the root to that node is called an ancestor of the node. {A, B} are the ancestor nodes of {E}.
Descendant: A node x is a descendant of another node y if and only if y is an ancestor of x.
Sibling: Children of the same parent node are called siblings. {D, E} are siblings.
Level of a Node: The number of edges on the path from the root node to that node. The root node is at level 0.
Internal Node: A node with at least one child is called an internal node.
Neighbor of a Node: Parent or child nodes of a node are called its neighbors.
Subtree: Any node of the tree along with all its descendants forms a subtree.

Advantages of Trees:

Efficient Searching: Trees are particularly efficient for searching and retrieving data. The time complexity of searching in AVL and Red-Black Trees is O(log n). This is better than arrays and linked lists, though not as fast as hashing. However, these trees provide the added benefit of maintaining sorted data and supporting operations like finding the floor and ceiling of values.
Fast Insertion and Deletion: Inserting and deleting nodes in self-balancing binary search trees like AVL and Red-Black Trees can be done in O(log n) time. While not faster than hashing, they offer ordered data and efficient floor/ceiling searches.
Hierarchical Representation: Trees provide a clear hierarchical structure, making it easy to organize and navigate large datasets.
Recursive Nature: Trees are naturally recursive and easy to traverse and manipulate using recursive algorithms.
Natural Organization: Trees naturally represent relationships like file systems, organizational charts, and taxonomies.
Flexible Size: Unlike arrays, trees can dynamically grow or shrink based on the number of nodes added or removed.

Disadvantages of Trees:

Memory Overhead: Trees can require significant memory, especially large ones, which can be problematic for memory-constrained applications.
Imbalanced Trees: An unbalanced tree can lead to inefficient operations with uneven search times.
Complexity: Trees are more complex to understand and implement than arrays or linked lists, posing challenges for beginners.
Search, Insert, and Delete Times: For operations limited to search, insert, and delete, hash tables are generally more efficient than self-balancing binary search trees.
Implementation Difficulty: Manipulating trees requires a good understanding of data structures and algorithms.

Representation of Tree in Memory

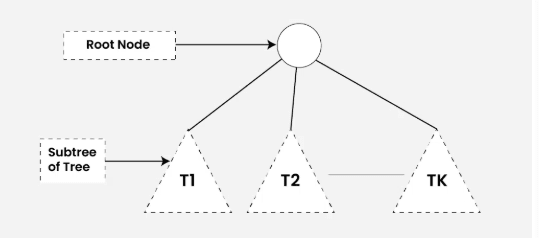
A tree consists of a root node and zero or more subtrees T₁, T₂, … , Tₖ such that there is an edge from the root node of the tree to the root node of each subtree. The subtree of a node X consists of all nodes that have X as an ancestor.

A tree can be represented using a collection of nodes. Each node can be defined using a class or struct as shown:

class Node {
public:
    int data;
    Node* first_child;
    Node* second_child;
    Node* third_child;
    .
    .
    .
    Node* nth_child;
};

Basic Operations of Tree Data Structure:

Create – Create a tree in the data structure
Insert – Insert data into the tree
Search – Search for specific data in the tree
Traversal:
- Depth-First Search (DFS) Traversal
- Breadth-First Search (BFS) Traversal

#include <bits/stdc++.h>
using namespace std;
 
void addEdge(int x, int y, vector<vector<int>>& adj) {
    adj[x].push_back(y);
    adj[y].push_back(x);
}
 
void printParents(int node, vector<vector<int>>& adj, int parent) {
    if (parent == 0)
        cout << node << "->Root" << endl;
    else
        cout << node << "->" << parent << endl;
 
    for (auto cur : adj[node])
        if (cur != parent)
            printParents(cur, adj, node);
}
 
void printChildren(int Root, vector<vector<int>>& adj) {
    queue<int> q;
    q.push(Root);
    int vis[adj.size()] = { 0 };
 
    while (!q.empty()) {
        int node = q.front();
        q.pop();
        vis[node] = 1;
        cout << node << "-> ";
        for (auto cur : adj[node])
            if (vis[cur] == 0) {
                cout << cur << " ";
                q.push(cur);
            }
        cout << endl;
    }
}
 
void printLeafNodes(int Root, vector<vector<int>>& adj) {
    for (int i = 1; i < adj.size(); i++)
        if (adj[i].size() == 1 && i != Root)
            cout << i << " ";
    cout << endl;
}
 
void printDegrees(int Root, vector<vector<int>>& adj) {
    for (int i = 1; i < adj.size(); i++) {
        cout << i << ": ";
        if (i == Root)
            cout << adj[i].size() << endl;
        else
            cout << adj[i].size() - 1 << endl;
    }
}
 
int main() {
    int N = 7, Root = 1;
    vector<vector<int>> adj(N + 1, vector<int>());
    addEdge(1, 2, adj);
    addEdge(1, 3, adj);
    addEdge(1, 4, adj);
    addEdge(2, 5, adj);
    addEdge(2, 6, adj);
    addEdge(4, 7, adj);
 
    cout << "The parents of each node are:" << endl;
    printParents(Root, adj, 0);
 
    cout << "The children of each node are:" << endl;
    printChildren(Root, adj);
 
    cout << "The leaf nodes of the tree are:" << endl;
    printLeafNodes(Root, adj);
 
    cout << "The degrees of each node are:" << endl;
    printDegrees(Root, adj);
 
    return 0;
}

Output:

The parents of each node are:
1->Root
2->1
5->2
6->2
3->1
4->1
7->4
The children of each node are:
1-> 2 3 4 
2-> 5 6 
3-> 
4-> 7 
5-> 
6-> 
7-> 
The leaf nodes of the tree are:
3 5 6 7 
The degrees of each node are:
1: 3
2: 2
3: 0
4: 1
5: 0
6: 0
7: 0

Properties of Tree Data Structure:

Number of Edges: An edge connects two nodes. If a tree has N nodes, it has N-1 edges. There's only one path from each node to any other node in the tree.
Depth of a Node: The number of edges on the path from the root to that node.
Height of a Node: The length of the longest path from the node to a leaf node.
Height of the Tree: The length of the longest path from the root to any leaf node.
Degree of a Node: The number of subtrees (children) attached to a node. A leaf node has a degree of 0. The degree of a tree is the maximum degree among all its nodes.

How's article quality?

Introduction

Representation of Tree in Memory

Page Contents